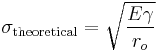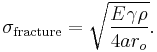Fracture
| Materials failure modes |
|---|
| Buckling |
| Corrosion |
| Creep |
| Fatigue |
| Fracture |
| Impact |
| Mechanical overload |
| Thermal shock |
| Wear |
| Yielding |
A fracture is the (local) separation of an object or material into two, or more, pieces under the action of stress.
The word fracture is often applied to bones of living creatures, or to crystals or crystalline materials, such as gemstones or metal. Sometimes, in crystalline materials, individual crystals fracture without the body actually separating into two or more pieces. Depending on the substance which is fractured, a fracture reduces strength (most substances) or inhibits transmission of light (optical crystals).
A detailed understanding of how fracture occurs in materials may be assisted by the study of fracture mechanics.
Contents |
Types of fracture
Brittle fracture


In brittle fracture, no apparent plastic deformation takes place before fracture. In brittle crystalline materials, fracture can occur by cleavage as the result of tensile stress acting normal to crystallographic planes with low bonding (cleavage planes). In amorphous solids, by contrast, the lack of a crystalline structure results in a conchoidal fracture, with cracks proceeding normal to the applied tension.
The theoretical strength of a crystalline material is (roughly)
where: -
 is the Young's modulus of the material,
is the Young's modulus of the material, is the surface energy, and
is the surface energy, and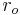 is the equilibrium distance between atomic centers.
is the equilibrium distance between atomic centers.
On the other hand, a crack introduces a stress concentration modeled by
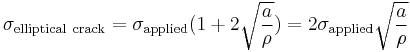 (For sharp cracks)
(For sharp cracks)
where: -
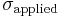 is the loading stress,
is the loading stress,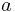 is half the length of the crack, and
is half the length of the crack, and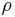 is the radius of curvature at the crack tip.
is the radius of curvature at the crack tip.
Putting these two equations together, we get
Looking closely, we can see that sharp cracks (small 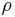 ) and large defects (large
) and large defects (large 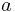 ) both lower the fracture strength of the material.
) both lower the fracture strength of the material.
Recently, scientists have discovered supersonic fracture, the phenomenon of crack motion faster than the speed of sound in a material. This phenomenon was recently also verified by experiment of fracture in rubber-like materials.
Ductile fracture


In ductile fracture, extensive plastic deformation takes place before fracture. Many ductile metals, especially materials with high purity, can sustain very large deformation of 50–100% or more strain before fracture under favorable loading condition and environmental condition. The strain at which the fracture happens is controlled by the purity of the materials. At room temperature, pure iron can undergo deformation up to 100% strain before breaking, while cast iron or high-carbon steels can barely sustain 3% of strain..
Because ductile rupture involves a high degree of plastic deformation, the fracture behavior of a propagating crack as modeled above changes fundamentally. Some of the energy from stress concentrations at the crack tips is dissipated by plastic deformation before the crack actually propagates.
The basic steps sample of smallest cross-sectional area), void formation, void coalescence (also known as crack formation), crack propagation, and failure, often resulting in a cup-and-cone shaped failure surface.
Crack separation modes

There are three ways of applying a force to enable a crack to propagate:
- Mode I crack – Opening mode (a tensile stress normal to the plane of the crack)
- Mode II crack – Sliding mode (a shear stress acting parallel to the plane of the crack and perpendicular to the crack front)
- Mode III crack – Tearing mode (a shear stress acting parallel to the plane of the crack and parallel to the crack front)
For more information, see fracture mechanics.
See also
- Bone fracture
- Brittle-ductile transition zone
- Environmental stress fracture
- Fracture mechanics
- Fracture (mineralogy)
- Fracture (geology)
- Fracture toughness
- Fractography
- Forensic engineering
- Forensic materials engineering
- Microvoid coalescence
- Rupture (engineering)
- Structural failure
Bibliography
- Dieter, G. E. (1988) Mechanical Metallurgy ISBN 0-07-100406-8
- A. Garcimartin, A. Guarino, L. Bellon and S. Cilberto (1997) " Statistical Properties of Fracture Precursors ". Physical Review Letters, 79, 3202 (1997)
- Callister, Jr., William D. (2002) Materials Science and Engineering: An Introduction. ISBN 0-471-13576-3
- Peter Rhys Lewis, Colin Gagg, Ken Reynolds, CRC Press (2004), Forensic Materials Engineering: Case Studies.
External links
- Web postings at http://www.jwave.vt.edu/crcd/farkas/lectures/Fract1/tsld006.htm
- Virtual museum of failed products at http://materials.open.ac.uk/mem/index.html
- Fracture and Reconstruction of a Clay Bowl
- Ductile fracture